Fig. 1 Muestra los datos experimentales (columna izquierda) y los coeficientes de ajuste para una ecuación de la forma Axb+C. Las diferentes curvas corresponden a diferentes longitudes (10,20,30,40,50 y 60cm) en un disipador de 7.6cm de ancho con Anodizado Negro y las aletas hacia abajo en disipación pasiva. [NOTA: Si la imagen se ve muy pequeña, se ve mucho mejor si la abres en una pestaña nueva]
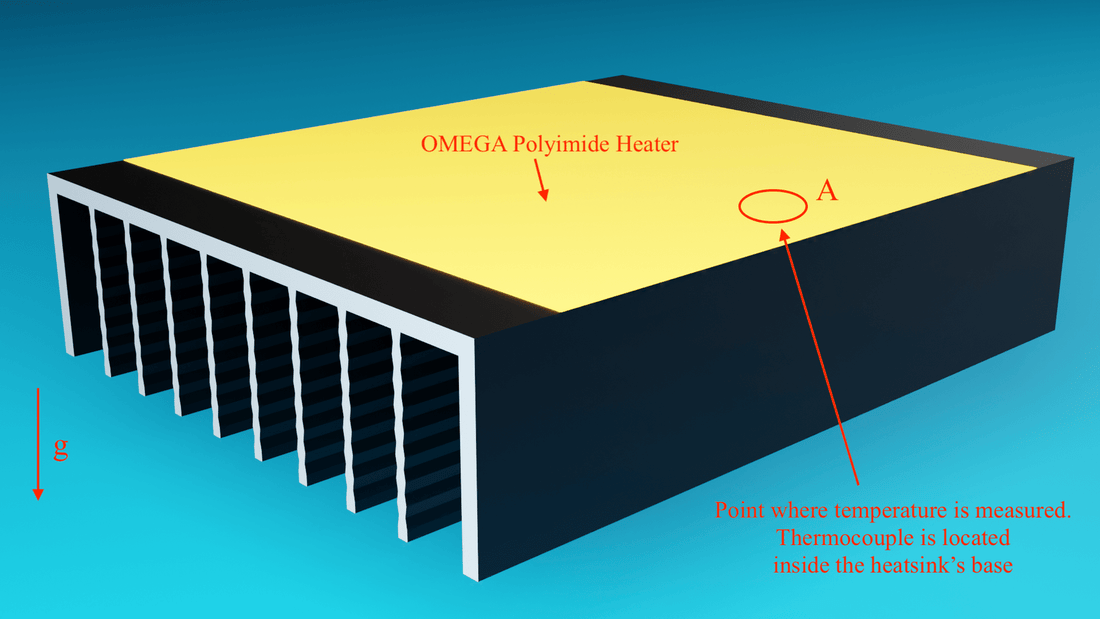
Fig. 2. Muestra el disipador usado para las pruebas. La flecha con letra 'g' indica la dirección de la gravedad. El punto A indica la zona donde realicé las mediciones de temperatura (el termopar va dentro de un orificio en la base del disipador, como se ve en la Fig. 3 de este otro post). La resistencia usada fue una OMEGA de poliamida de 7.6cm x 7.6cm modelo KHVLA-303/10. La resistencia siempre está ubicada a la mitad del disipador para todas las longitudes.
Este post es el número 2 de 4 donde presento las temperaturas que alcanza un disipador de 7.6cm de ancho a diferentes potencias y con diferentes longitudes. Cada post cubre una orientación diferente. En este caso, las aletas apuntan hacia abajo (disipación pasiva)
Para ver la explicación más detallada, puedes ver el Primer Post.
Abajo presento las ecuaciones de ajuste para las mediciones que presento en la Fig. 1
| Longitud (cm) | Ecuación de Resistencia Térmica |
| 20 | T = 3.890 * W 0.789 + 24.55 |
| 30 | T = 3.008 * W 0.814 + 24.55 |
| 40 | T = 2.319 * W 0.852 + 24.68 |
| 50 | T = 2.120 * W 0.856 + 24.43 |
| 60 | T = 1.929 * W 0.874 + 24.58 |
Tabla 1. Muestra las ecuaciones que predicen la temperatura del disipador en función del calor entregado. La variable W corresponde a la cantidad de calor entregado al disipador y T es la temperatura del disipador en el punto A [Fig.2]. Calibrado a una temperatura ambiente de 25ºC.
Observaciones:
1) Todas las temperaturas están normalizadas a 25ºC. Para obtener la temperatura del disipador correspondiente a una temperatura ambiente diferente, solo hay que sumar o restar la diferencia con respecto a 25ºC. Ejemplo: La ecuación para una longitud de 20cm predice una temperatura de 110ºC para una cantidad de calor de 50W a una temp. ambiente de 25ºC. Para una temp. ambiente de 30ºC, la temperatura sería de 115ºC.