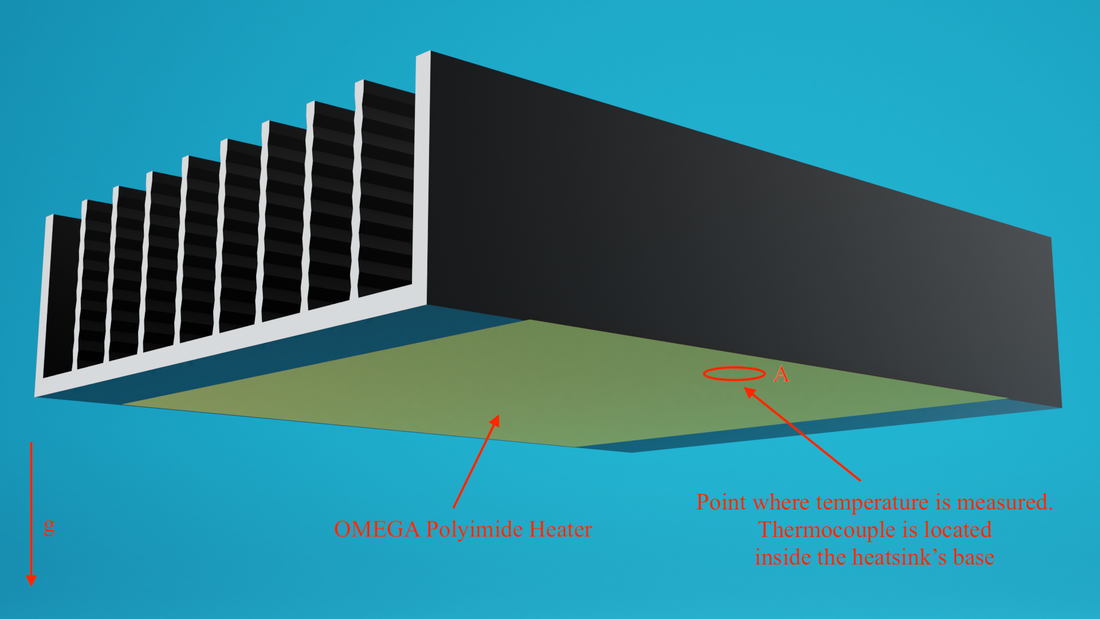
Fig. 2. Muestra el disipador usado para las pruebas. La flecha con letra 'g' indica la dirección de la gravedad. El punto A indica la zona donde realicé las mediciones de temperatura (el termopar va dentro de un orificio en la base del disipador, como se ve en la Fig. 3 de este otro post). La resistencia usada fue una OMEGA de poliamida de 7.6cm x 7.6cm modelo KHVLA-303/10. La resistencia siempre está ubicada a la mitad del disipador para todas las longitudes.
En este blog post presento las ecuaciones que pueden ayudar a predecir la temperatura que alcanzaría el disipador de 7.6cm en longitudes de 20,30,40,50 y 60cm.
Para todas las longitudes de la Fig.1 realicé las mediciones con un termopar dentro de la base del disipador (punto A de la Fig. 2). El elemento eléctrico que genera el calor es una resistencia de poliamida OMEGA de 7.6cm x 7.6cm.
En general, la resistencia térmica de un disipador comercial se presenta como el coeficiente de una ecuación lineal Ax + b [Ec. 1], donde A es el coeficiente que representa la resistencia térmica, x es la potencia en calor entregada por el dispositivo y b idealmente sería la temperatura ambiente (cuando x=0)
Sin embargo, en todas las mediciones que he realizado con el tiempo y en el caso de disipación pasiva, un ajuste lineal no parece adecuado sobre todo cuando se incluyen potencias de calor entregado entre 5 y 10W.
Es por ello que mejor opté por generar un ajuste con una ecuación potencial que tuviera un mejor acercamiento a los datos experimentales, pues es de mayor utilidad para mis clientes.
La ecuación potencial tiene la forma Axb+C [Ec. 2]. La Fig.1 contiene los datos experimentales así como las líneas de ajuste y las gráficas con los coeficientes de la Ec.2.
Para mayor claridad, a continuación presento las ecuaciones completas con sus respectivas longitudes.
| Longitud (cm) | Ecuación de Resistencia Térmica |
| 20 | T = 3.508 * W 0.795 + 24.76 |
| 30 | T = 2.780 * W 0.810 + 24.73 |
| 40 | T = 2.194 * W 0.843 + 24.80 |
| 50 | T = 2.048 * W 0.848 + 24.59 |
| 60 | T = 1.855 * W 0.864 + 24.72 |
Tabla 1. Muestra las ecuaciones que predicen la temperatura del disipador en función del calor entregado. La variable W corresponde a la cantidad de calor entregado al disipador y T es la temperatura del disipador en el punto A [Fig.2]. Calibrado a una temperatura ambiente de 25ºC.
Observaciones:
1) Todas las temperaturas están normalizadas a 25ºC. Para obtener la temperatura del disipador correspondiente a una temperatura ambiente diferente, solo hay que sumar o restar la diferencia con respecto a 25ºC. Ejemplo: La ecuación para una longitud de 20cm predice una temperatura de 103ºC para una cantidad de calor de 50W a una temp. ambiente de 25ºC. Para una temp. ambiente de 30ºC, la temperatura sería de 108ºC.